2. Perceptron Learning Algorithm

预期收益

• ☆ 感知机学习算法面临的困难
• ★ 能够表述感知机迭代基本思想及迭代公式几何意义
• ☆ PLA 算法存在哪些疑问

时间成本

• 阅读 05 分钟
• 思考 10 分钟

2.1. 设计感知机学习算法面临的困难

• 样本标签列取值, \(\mathcal{Y}=\{-1, 1\}\)
• 训练集合\(\mathcal{D}\)中, 第\(i\) 的样本记为\(x_{i}\), 标签列取值记为\(y_{i}\)

2.1.1. 感知机学习算法的目标

几何意义

• 由感知机的假设空间可知, 感知机中的假设对应多维空间中的超平面.
• 若某一超平面将样本数据正确的将样本点分成两个半平面, 这样的超平面就是我们最终要寻找的解.

数学表达

• 感知机的假设的一般形式\(h(x)=sign(w \cdot x)\), 当权重向量\(w\)一旦确定, 假设函数也就确定.

• 目标就是找出\(w\), 使得所有的历史数据集合\(\mathcal{D}\)都能用找到的假设函数去正确分类

  此假设在集合\(\mathcal{D}\)上, \(h(x_i) = y_i\), 即\(y_i = sign(w \cdot x_i)\), 或\(y_i (w \cdot x_i) > 0\)

2.1.2. 困难

• 寻找最接近目标函数的假设, 首先, 要保证假设函数在历史数据集上能够正确的分类
• 假设空间包含无数个可能的假设, 直接遍历不可能

2.2. 感知机学习算法的步骤

注解

核心思想, 知错能改, 善莫大焉

• 知错

  给定一个假设函数, 找到一个不能正确分类的样本点, 即\(y \neq sign(w \cdot x)\), 或\(y (w \cdot x) < 0\)

• 能改

  设定恰当的策略, 让当前不能分类的样本点有可能分对, 不能分类正确的样本点\(y (w \cdot x) < 0\)

  1. 正例分成了负例, \(y=1\), \(w \cdot x < 0\),

     向量\(x, w\)之间的夹角太大, 我们要调整向量\(w' = w + x = w + yx\), 使得两向量的夹角变小

  2. 负例分成了正例, \(y=-1\), \(w \cdot x > 0\),

     向量\(x, w\)之间的夹角太小, 我们要调整向量\(w' = w - x = w + yx\), 使得两向量的夹角变大

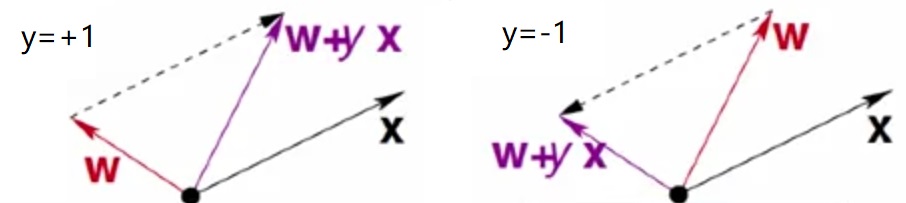
2.2.1. 步骤

1. 第\(t=1, 2, \ldots\)次迭代过程

   • 找到一个分类错误的样本

     • 遍历样本集合, 记为\(x_{n(t)}\)

   • 迭代

     • \(w_{t+1} = w_{t} + y_{n(t)}x_{n(t)}\)

2.3. PLA 疑问

1. PLA 一定可以终止吗? 什么情况下能够终止?
2. PLA 迭代步数和哪些因素相关, 可以给出迭代步数上限吗?
3. PLA 即使能够终止, 只能说明, 找到的假设函数在历史数据集上表现好, 能够说明找到的假设就一定是目标函数吗?

我们会在接下来的章节详细探讨上述问题