2.3. 感知机学习算法PLA有效性前提¶
预期收益
- ★ PLA 终止的前提条件
- ☆ 可以举例说明, 什么是线性可分、线性不可分
- ★ PLA 在线性可分数据集上, 迭代次数上限估计
时间成本
- 阅读 05 分钟
- 思考 10 分钟
2.3.1. PLA 终止的前提条件¶
感知机的求解目标
- 在假设空间上(无数超平面), 找到一个可以将历史数据集正确分类的超平面
- 如果, 历史数据集\(\mathcal{D}\)上, 本来就不存在这样的超平面, 称\(\mathcal{D}\)线性不可分, 无论用什么算法都学习不到超平面, 所以PLA无法达到终止条件
- 如果, 历史数据集\(\mathcal{D}\)上, 存在可以将样本正确分类的超平面, 称\(\mathcal{D}\)线性可分, 此时数据那用PLA有可能达到终止条件, 是否一定能够通过有限次迭代学习到呢?
线性可分, 线性不可分示例
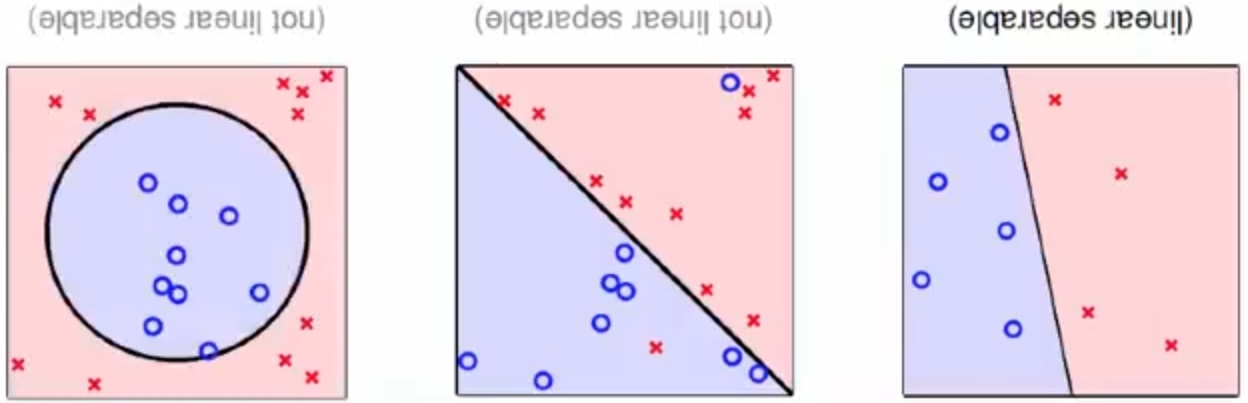
PLA 能够有效学习的前提条件是数据集线性可分
2.3.2. PLA 迭代次数估计¶
2.3.2.1. 符号说明¶
- \(w_{f}\), 目标函数\(f(x)\)对应的权重系数
- \(w_{t}\), 第\(t\)次迭代对应的权重系数
- \((x_{n(t)}, y_{n(t)})\), 第\(t\)次迭代, 误分类的样本点
显然有
- \(y_{n(t)} \neq sign(w_{t} \cdot x_{n(t)})\), 即\(y_{n(t)} (w_{t} \cdot x_{n(t)}) < 0\)
- \(y_{n(t)} (w_{f} \cdot x_{n(t)}) > 0\)
- \(w_{t+1} = w_{t} + y_{n(t)}x_{n(t)}\)
我们在初始化时, 不失一般性\(w_{0}=\mathbf{0}\)
2.3.2.2. \(w_{t}\)和\(w_{f}\)内积¶
两个向量的内积大小可以在一定程度上反映两个向量相似性(夹角大小), \(w_{f} \cdot w_{t} = \|{w_{f}}\|\|w_{t}\|\cos\theta\)
在迭代的过程中我们有如下结论: \(w_{f} \cdot w_{t+1} > w_{f} \cdot w_{t}\), 在一定程度上说明, 每迭代一次, 学习到的权重更接近目标权重
\[\begin{split}\begin{array}{lll}
w_{f} \cdot w_{t+1} &=& w_{f} \cdot (w_{t} + y_{n(t)}x_{n(t)}) \\
&=& w_{f} \cdot w_{t} + y_{n(t)}w_{f}x_{n(t)} \\
&>& w_{f} \cdot w_{t}
\end{array}\end{split}\]
同时有
\[\begin{split}\begin{array}{lll}
w_{f} \cdot w_{t+1} &=& w_{f} \cdot (w_{t} + y_{n(t)}x_{n(t)}) \\
&=& w_{f} \cdot w_{t} + y_{n(t)}w_{f}x_{n(t)} \\
&=& w_{f} \cdot w_{0} + \sum_{i=0}^t{y_{n(t)}w_{f}x_{n(t)}}
&=& \sum_{i=0}^t{y_{n(t)}w_{f}x_{n(t)}}
\end{array}\end{split}\]
2.3.2.3. \(w_{t}\) 范数上限估计¶
\[\begin{split}\begin{array}{lll}
\|w_{t+1}\|^2 &=& \|w_{t} + y_{n(t)}x_{n(t)}\|^2 \\
&=& \|w_{t}\|^2 + 2y_{n(t)}w_{t} \cdot x_{n(t)} + \|y_{n(t)}x_{n(t)}\|^2 \\
&\lt& \|w_{t}\|^2 + 0 + \|x_{n(t)}\|^2 \\
&\leq& \|w_{t}\|^2 + \max_{x \in \mathcal{D}}\|x\|^2 \\
&\lt& \|w_{t-1}\|^2 + 2R^2 \\
&\lt& \|w_{0}\|^2 + (t+1)R^2 \\
&=& (t+1)R^2
\end{array}\end{split}\]
其中\(R^2 = \max_{x \in \mathcal{D}}\|x\|^2\)
2.3.2.4. \(w_{t}\)和\(w_{f}\)夹角¶
由于两个单位法向量的夹角最小为0, 从而有
\[\begin{split}\begin{array}{lll}
1 &\geq& \frac{w_{f}}{\|w_{f}\|} \cdot \frac{w_{t}}{\|w_{t}\|} \\
&\gt& \frac{w_{f}}{\|w_{f}\|} \cdot \frac{w_{t}}{\sqrt{t}R} \\
&=& \frac{w_{f} \cdot w_{t}}{\|w_{f}\|\sqrt{t}R} \\
&=& \frac{\displaystyle\sum_{i=0}^{t-1}{y_{n(i)}w_{f}x_{n(i)}}}{\|w_{f}\|\sqrt{t}R} \\
&\geq& \frac{\displaystyle\sum_{i=0}^{t-1}{y_{n(i)}\frac{w_{f}}{\|w_{f}\|}x_{n(i)}}}{\sqrt{t}R} \\
&\geq& \frac{\displaystyle\sum_{i=0}^{t-1}{\displaystyle\min_{n}{y_{n}\frac{w_{f}}{\|w_{f}\|}x_{n}}}}{\sqrt{t}R} \\
&=& \frac{t\displaystyle\min_{n}{y_{n}\frac{w_{f}}{\|w_{f}\|}x_{n}}}{\sqrt{t}R} \\
&=& \frac{\sqrt{t}}{R}\displaystyle\min_{n}{y_{n}\frac{w_{f}}{\|w_{f}\|}x_{n}} \\
&=& \sqrt{t}\frac{\rho}{R}
\end{array}\end{split}\]
其中\(\rho=\displaystyle\min_{n}{y_{n}\frac{w_{f}}{\|w_{f}\|}x_{n}}\)
上式说明, 随着迭代步数的增加, \(w_{t}\)和\(w_{f}\)的内积下限在不断增大(夹角在减小, \(\cos\theta\)在增大). 并且其下限和迭代次数的\(\sqrt{t}\)成正比
2.3.2.5. 迭代次数上限估计¶
\[\begin{array}{lll}
t &\leq& \frac{R^2}{\rho^2}
\end{array}\]
从而有, 一旦数据集可分, PLA一定可以通过有限次迭代, 使得学习到权重向量就是目标函数的权重向量