1. Perceptron 假设空间

预期收益

• ★ 可以通过举例说明感知机模型的基本思想, 加权打分, 看总分值是否超过设定阈值作为划分类别的依据
• ★ 能够写出感知机假设函数的一般形式, 形式统一化, 处理阈值过程的小技巧
• ★ 可以用可视化的方式, 解释假设函数的含义

时间成本

• 阅读 05 分钟
• 思考 10 分钟

1.1. 感知机的基本思想

1.1.1. 生活中评价事物的一般方法

根据过往的经验, 来判断某一事物的价值/能力/…,

1. 我们从某个事物的各个纬度去和同类事物作对比, 然后在每一纬度进行打分
2. 加权汇总各纬度的值, 汇总值作为事物的最终分数
3. 最终分数和我们划定的标准作比较, 然后分为达标/不达标, 优秀/一般, …

示例

• 某位考生是否达到录取分数线
• 跳水项目, 评委给运动员打分, 从技术难以程度, 动作姿势完成度, …

1.1.2. 信用卡审核是否通过

我们在考虑信用卡申请是否成功的过程中, 根据用户申请信息的各纬度的特征,

用户	年龄	年收入	负债	工龄
张三	29	25W	3W	6
李四	25	16W	1W	2
王五	30	42W	68W	8

我们试图按着上述思想给每个用户按各个纬度进行打分, 最后汇总每个用户的得分, 分值高过某个特定值时, 通过审核, 否则未通过审核

需要注意的是, 我们这里特征并不一定都是加分项, 比如, 负债可能作为减分项, 此时负责的权重系数可以为负的

1.2. 感知机假设函数的基本形式

\[\begin{split}\begin{array}{lll} h(x) &=& sign(\displaystyle\sum_{i=1}^n{w_i*x_i} - threshold) \\ &=& sign(\displaystyle\sum_{i=1}^n{w_i*x_i} - threshold * 1) \\ &=& sign(\displaystyle\sum_{i=1}^n{w_i*x_i} + w_0 * x_0) \\ &=& sign(\displaystyle\sum_{i=0}^n{w_i*x_i}) \\ &=& sign(w \cdot x) \end{array}\end{split}\]

其中, \(w_0 = - threshold\), \(x_0 = 1\)

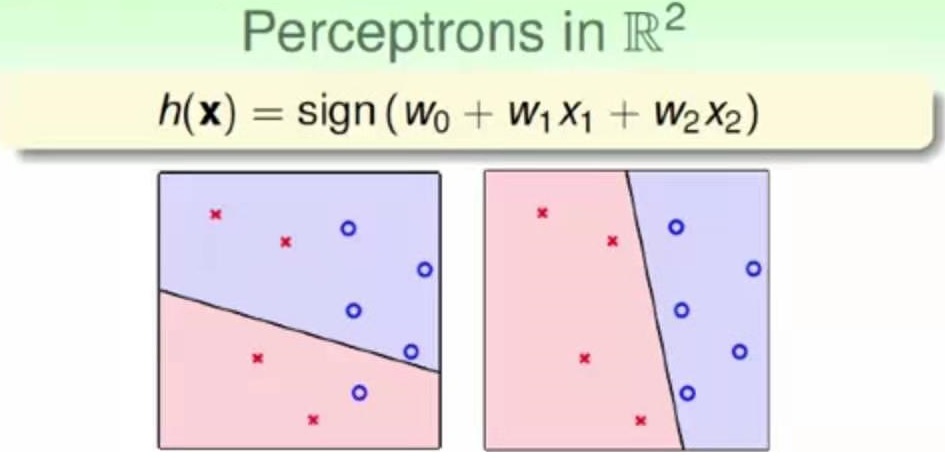
1.3. 假设函数的几何意义

• 如果只有两维特征的时候, \(h(x)=sign(\sum_{i=0}^2{w_i*x_i})\)
• 显然\(\sum_{i=0}^2{w_i*x_i}=0\)构成平面内一条直线, 将平面划分成两部分
• 点落在一侧半平面为通过信用卡审核, 另一侧为未通过审核